20188번: 등산 마니아
동네 뒷 산에는 등산로가 있다. 등산로는 N개의 작은 오두막들이 N −1개의 오솔길로 이어진 형태이다. 한 오솔길은 두 개의 오두막을 양 방향으로 연결한다. 한 오솔길의 길이는 1이다. 어떤 오
www.acmicpc.net
무난한 트리 DP라고 생각했는데 풀고 나니 DP를 쓰지 않았더라. 나처럼 푼 사람이 거의 없는 듯해서 풀이를 한번 소개해보려 한다.
(어쩐지 어렵더라)
풀이의 전체적인 틀은 트리 dp할 때와 비슷하다. dfs를 돌면서 서브 트리에 대해 문제를 해결한 다음, 이를 합쳐서 전체 트리에 대한 문제를 해결한다. 하지만 이때 서브 트리에서 전해주는 값이 조금 다를 뿐이다.
다음과 같은 상황을 가정해보자.

깊이가 $d$인 노드 $p$를 루트 노드로 하는 서브 트리의 답을 계산할 것이다. 이때 서브 트리 $a$에는 깊이가 각각 $a_{1},a_{2}, \cdots , a_{x}$ 인 노드 $x$개가 있고, 서브 트리 $b$에는 깊이가 각각 $b_{1},b_{2}, \cdots , b_{y}$ 인 노드 $y$개가 있다.
크게 세 경우로 나눠서 계산할 수 있다.
1. 서브 트리 $a$의 노드와 노드 $p$의 다양성
2. 서브 트리 $b$의 노드와 노드 $p$의 다양성
3. 서브 트리 $a$의 노드와 서브 트리 $b$의 노드의 다양성
1번은 $a_{1}+a_{2}+ \cdots +a_{x}$, 2번은 $b_{1}+b_{2}+ \cdots +b_{y}$ 로 쉽게 표현할 수 있다.
3번을 생각해보자. 먼저 깊이가 $a_{1}$인 노드와 깊이가 $b_{1}$인 노드의 다양성은 $a_{1}+b_{1}-d$ 이다.
이런 식으로 모든 노드들을 짝지어주면 $a_{i}$는 $y$번, $b_{i}$는 $x$번 더해지고 $d$는 $xy$번 빼진다는 것을 알 수 있다.
따라서 3번의 총합은 $y(a_{1}+a_{2}+ \cdots +a_{x})+x(b_{1}+b_{2}+ \cdots +b_{x})-xyd$ 이다.
$a_{1}+a_{2}+ \cdots +a_{x}=sum_{a}$, $b_{1}+b_{2}+ \cdots +b_{y}=sum_{b}$ 라고 하면
서브 트리 $p$의 답은 $sum_{a}+sum_{b}+y\cdot sum_{a}+x\cdot sum_{b}-xyd$ 이다.
아직 문제를 풀기에는 부족해 보인다.
노드 $p$의 자식을 3개로 확장해보자.
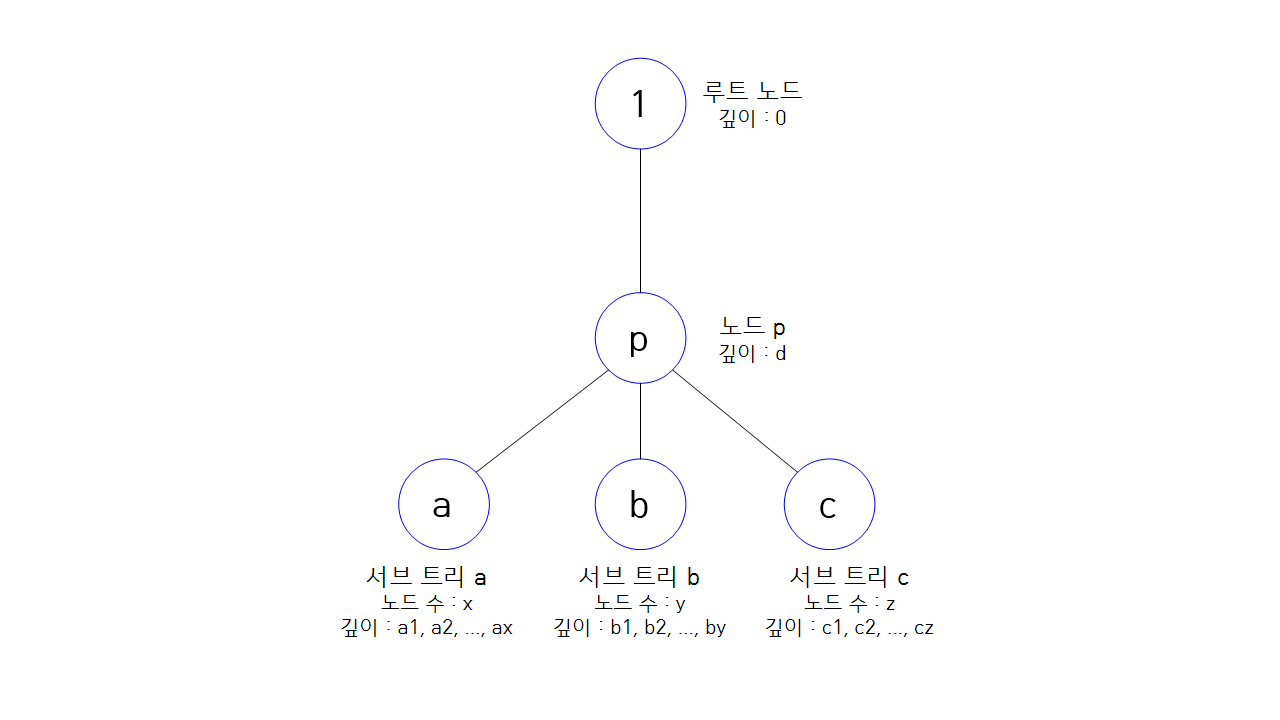
마찬가지로 노드 $p$와 서브 트리 간의 다양성의 합은 $sum_{a}+sum_{b}+sum_{c}$ 이다.
서브 트리 $a$, 서브 트리 $b$ 간의 다양성의 합은 $y\cdot sum_{a}+x\cdot sum_{b}-xyd$,
서브 트리 $b$, 서브 트리 $c$ 간의 다양성의 합은 $z\cdot sum_{b}+y\cdot sum_{c}-yzd$,
서브 트리 $c$, 서브 트리 $a$ 간의 다양성의 합은 $x\cdot sum_{c}+z\cdot sum_{a}-zxd$ 이다.
따라서 서브 트리 p의 답은 다음과 같다.
$(sum_{a}+sum_{b}+sum_{c})+(y\cdot sum_{a}+x\cdot sum_{b}-xyd)+(z\cdot sum_{b}+y\cdot sum_{c}-yzd)+(x\cdot sum_{c}+z\cdot sum_{a}-zxd)$
$= sum_{a}+sum_{b}+sum_{c}+(x+y)\cdot sum_{a}+(y+z)\cdot sum_{b}+(z+x)\cdot sum_{c}-(xy+yz+zx)\cdot d$
$= sum_{a}+sum_{b}+sum_{c}+(x+y+z)(sum_{a}+sum_{b}+sum_{c})-x\cdot sum_{a}-y\cdot sum_{b}-z\cdot sum_{c}-(xy+yz+zx)\cdot d$
$= (x+y+z+1)(sum_{a}+sum_{b}+sum_{c})-x\cdot sum_{a}-y\cdot sum_{b}-z\cdot sum_{c}-(\frac{(x+y+z)^2-x^2-y^2-z^2}{2})\cdot d$
자식이 $k$개일 때의 일반식도 마찬가지의 과정을 거치면 쉽게 도출할 수 있으나, 굳이 하지는 않겠다.
이제 문제를 풀 수 있다. dfs를 돌면서 노드의 수와 깊의 합을 누적해주고, 모든 노드에서 그 노드를 루트로 하는 서브 트리의 답을 구한다. 그러면 이들의 합이 전체 경로의 다양성의 합이 된다.
#include<bits/stdc++.h>
using namespace std;
#define fastio ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define X first
#define Y second
typedef long long ll;
typedef pair<ll,ll> pll;
const int N=3e5+1;
vector<int> ad[N];
ll dep[N],ans;
pll dfs(int cur,int prv) {
dep[cur]=dep[prv]+1;
pll ret={0,0}; ll sq=0;
for(auto nxt : ad[cur]){
if(nxt==prv) continue;
auto now=dfs(nxt,cur);
ret.X+=now.X, ret.Y+=now.Y;
ans-=now.X*now.Y;
sq+=now.Y*now.Y;
}
ans+=ret.X*(ret.Y+1)-dep[cur]*(ret.Y*ret.Y-sq)/2;
ret.X+=dep[cur], ret.Y+=1;
return ret;
}
int main()
{
fastio;
int n; cin >> n;
for(int i=1;i<n;i++){
int u,v; cin >> u >> v;
ad[u].push_back(v);
ad[v].push_back(u);
}
dep[0]=-1;
dfs(1,0);
cout << ans;
}'Problem Solving > Baekjoon OJ' 카테고리의 다른 글
| Ruby V (3) | 2021.08.31 |
|---|---|
| Class 9 (4) | 2021.08.29 |
| Diamond I 달성 (5) | 2021.07.03 |
| [BOJ 2867] 수열의 값 (2) | 2021.06.12 |
| Diamond II 달성 (4) | 2021.05.30 |


